डेटा संरचना में एल्गोरिदम का विश्लेषण

परिचय

डेटा संरचना में एल्गोरिदम का विश्लेषण कंप्यूटर विज्ञान की एक मूलभूत अवधारणा है। जब भी हम डेटा संरचना का उपयोग करके किसी समस्या को हल करते हैं, तो हम उसके लिए एक एल्गोरिदम डिज़ाइन करते हैं। लेकिन केवल एल्गोरिदम लिखना ही पर्याप्त नहीं है—हमें इसकी दक्षता का मापन भी करना होता है। इस मापन को एल्गोरिदम का विश्लेषण कहा जाता है, और यह हमें समय और मेमोरी के संदर्भ में किसी प्रोग्राम के प्रदर्शन को समझने में मदद करता है।.

डेटा संरचना में एल्गोरिदम का विश्लेषण क्या है?

डेटा संरचना में एल्गोरिदम का विश्लेषण करने का अर्थ है, एल्गोरिदम द्वारा उपयोग किए जाने वाले संसाधनों के आधार पर उसका मूल्यांकन करना। दो प्रमुख संसाधन हैं:

• समय – एल्गोरिदम कितनी तेजी से चलता है।.
• स्पेस – एल्गोरिदम को कितनी मेमोरी की आवश्यकता है।.
  

इनका विश्लेषण करके, हम एक ही समस्या के लिए विभिन्न एल्गोरिदम की तुलना कर सकते हैं और यह तय कर सकते हैं कि कौन सा अधिक उपयुक्त है।.

उदाहरण के लिए, यदि हम किसी सूची में किसी तत्व को खोजना चाहते हैं, तो हम रैखिक खोज या बाइनरी खोज का उपयोग कर सकते हैं। दोनों से सही उत्तर मिलेगा, लेकिन क्रमबद्ध डेटा होने पर बाइनरी खोज तेज़ होती है। यह अंतर केवल उनकी समय जटिलता का विश्लेषण करने पर ही स्पष्ट होता है।.

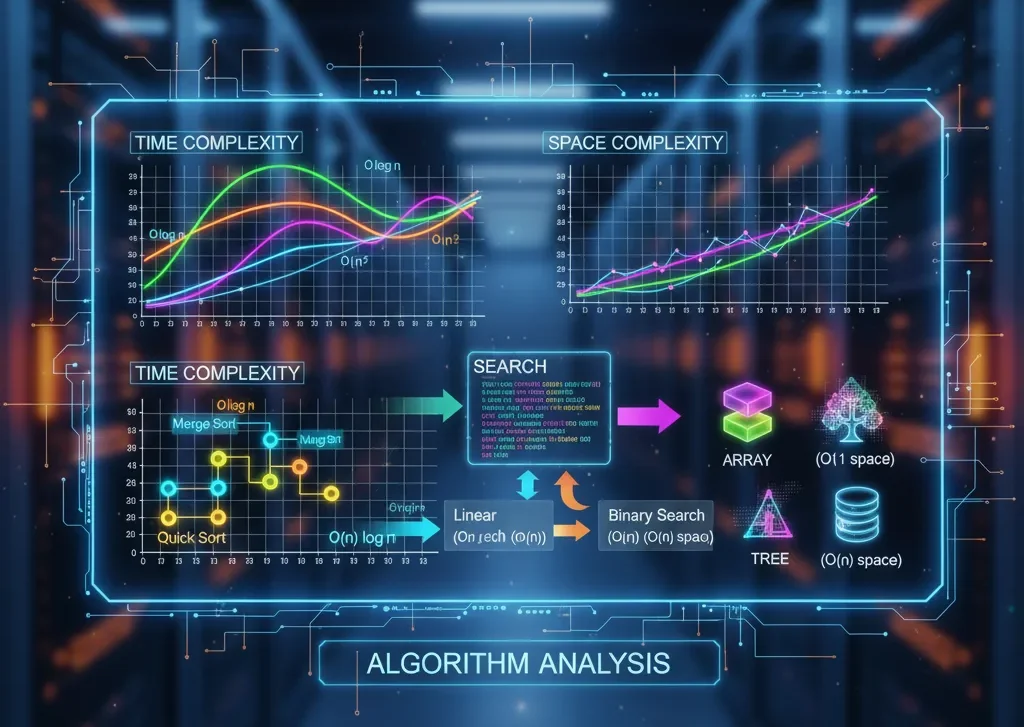
एल्गोरिदम के विश्लेषण की आवश्यकता

डेटा संरचना में एल्गोरिदम का विश्लेषण महत्वपूर्ण है क्योंकि:

• यह हमें किसी एल्गोरिदम को चलाने से पहले उसके व्यवहार का अनुमान लगाने में मदद करता है।.
• यह हमें एक ही समस्या को हल करने वाले दो या दो से अधिक एल्गोरिदम की तुलना करने की अनुमति देता है।.
• यह सुनिश्चित करता है कि बड़े इनपुट के साथ भी कार्यक्रम कुशल हों।.
• यह वास्तविक दुनिया के अनुप्रयोगों के लिए सही डेटा संरचना और एल्गोरिदम का चयन करने में मदद करता है।.

उचित विश्लेषण के बिना, कोई एल्गोरिदम छोटे डेटा के लिए तो काम कर सकता है लेकिन इनपुट का आकार बढ़ने पर विफल हो सकता है।.

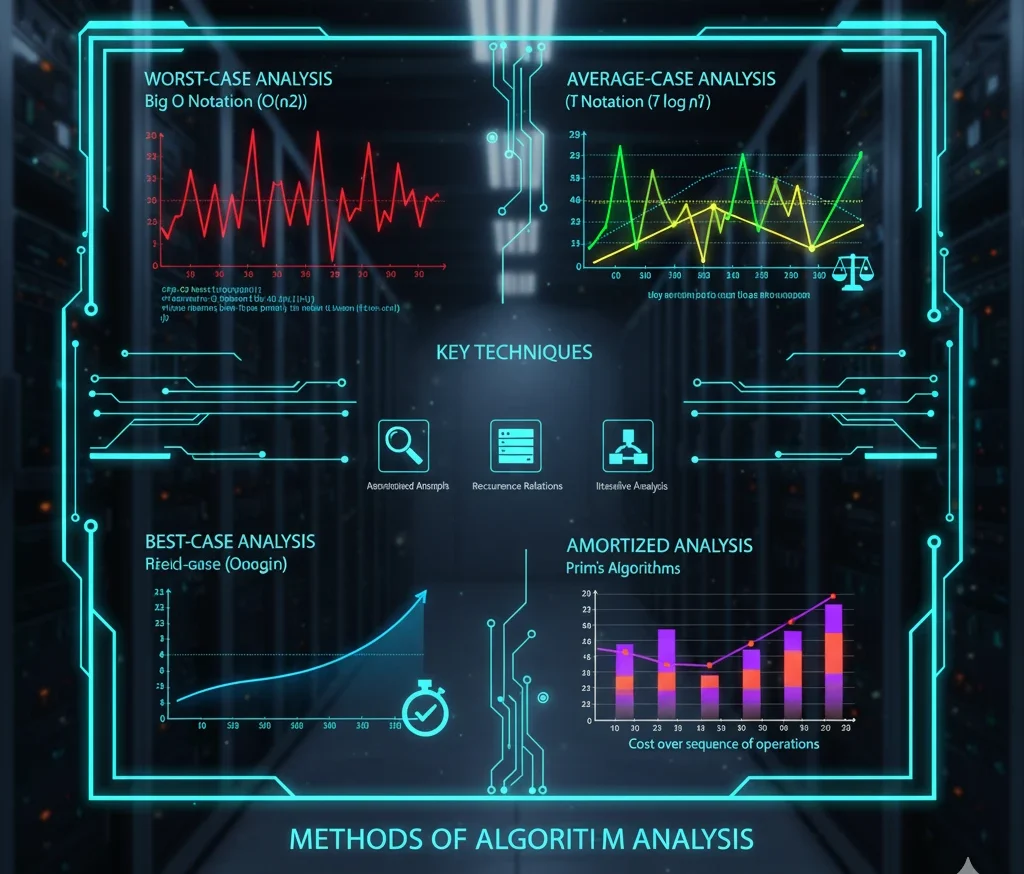
विश्लेषण के तरीके

एल्गोरिदम का विश्लेषण करने के तीन मानक तरीके हैं:

1. सर्वोत्तम स्थिति विश्लेषण – एल्गोरिदम द्वारा लिया गया न्यूनतम समय।.
      उदाहरण: लीनियर सर्च में, यदि तत्व पहले स्थान पर पाया जाता है।.
2. सबसे खराब स्थिति का विश्लेषण – एल्गोरिदम द्वारा लिया गया अधिकतम समय।.
      उदाहरण: लीनियर सर्च में, यदि एलिमेंट अंतिम स्थान पर है या नहीं मिला है।.
3. औसत केस विश्लेषण – यादृच्छिक इनपुट के लिए अपेक्षित चलने का समय।.
   उदाहरण: लीनियर सर्च में, एलिमेंट औसतन कहीं बीच में होता है।.

समय जटिलता यह बताती है कि इनपुट के आकार के साथ एल्गोरिदम के चलने का समय कैसे बढ़ता है। इसे गणितीय संकेतों का उपयोग करके व्यक्त किया जाता है जैसे:

समय जटिलता यह बताती है कि इनपुट के आकार के साथ एल्गोरिदम के चलने का समय कैसे बढ़ता है। इसे गणितीय संकेतों का उपयोग करके व्यक्त किया जाता है जैसे:

• O(1) – स्थिर समय (इनपुट आकार से स्वतंत्र)।.
• O(log n) – लघुगणकीय समय (बाइनरी खोज)।.
• O(n log n) – लॉग-रेखीय समय (मर्ज सॉर्ट, क्विकसॉर्ट)।.
• O(n²) – द्विघात समय (बबल सॉर्ट, सिलेक्शन सॉर्ट)।.
• O(n) – रैखिक समय (रैखिक खोज)।.

ये संकेतन डेटा संरचना में एल्गोरिदम के विश्लेषण की रीढ़ की हड्डी हैं।.

विश्लेषण में स्थानिक जटिलता

स्पेस कॉम्प्लेक्सिटी से तात्पर्य उस मेमोरी की मात्रा से है जिसकी आवश्यकता किसी एल्गोरिदम को निष्पादित करने के लिए होती है। इसमें शामिल हैं:

• चरों के लिए स्मृति।.
• डेटा संरचनाओं के लिए मेमोरी।.
• पुनरावर्तन या फ़ंक्शन कॉल के लिए मेमोरी।.

उदाहरण के लिए, मर्ज सॉर्ट एरे को मर्ज करने के लिए अतिरिक्त मेमोरी का उपयोग करता है, जबकि क्विकसॉर्ट ज्यादातर एक ही एरे के भीतर काम करता है, जिससे यह अधिक स्पेस एफिशिएंट होता है।.

डेटा संरचनाओं में उदाहरण

खोज रहे हैं:

• रैखिक खोज → O(n)
• बाइनरी सर्च → O(log n)

छँटाई:

• बबल सॉर्ट → O(n²)
• मर्ज सॉर्ट → O(n log n)

ट्री ऑपरेशन:

• बाइनरी सर्च ट्री में सर्च करना → औसत स्थिति में O(log n), सबसे खराब स्थिति में O(n)।.

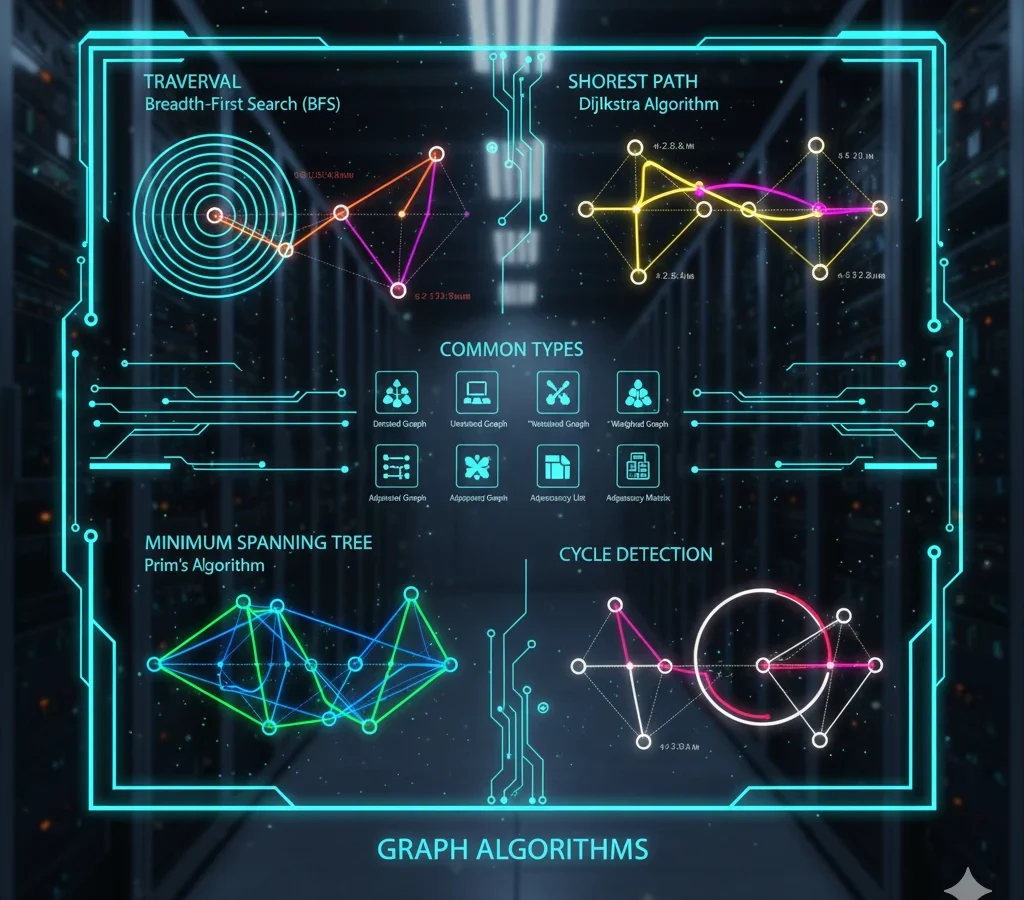
ग्राफ एल्गोरिदम:

• ब्रॉडथ-फर्स्ट सर्च (बीएफएस) → O(V + E) जहाँ V = वर्टेक्स, E = एज।.

ये उदाहरण दर्शाते हैं कि डेटा संरचना में एल्गोरिदम का विश्लेषण वास्तविक अनुप्रयोगों के प्रदर्शन को सीधे तौर पर कैसे प्रभावित करता है।.

निष्कर्ष

डेटा संरचना में एल्गोरिदम का विश्लेषण कुशल प्रोग्राम लिखने के लिए आवश्यक है। यह हमें समय जटिलता, स्थान जटिलता का मूल्यांकन करने और एक ही समस्या के लिए विभिन्न दृष्टिकोणों की तुलना करने में मदद करता है। विश्लेषण के बिना, हम स्केलेबिलिटी और प्रदर्शन सुनिश्चित नहीं कर सकते।.

कंप्यूटर विज्ञान में, सही समाधान ही पर्याप्त नहीं है; यह कुशल भी होना चाहिए। इसीलिए एल्गोरिदम का विश्लेषण हमेशा डेटा संरचनाओं के साथ मिलकर किया जाता है।.

जिस प्रकार एल्गोरिदम को कुशलतापूर्वक कार्य करने के लिए उचित विश्लेषण की आवश्यकता होती है, उसी प्रकार डेटाबेस भी अच्छी तरह से परिभाषित मानदंडों पर निर्भर करते हैं। attributes in database to give meaning and structure to stored data.