Data Structures & Algorithms (DSA) – Dynamic Programming Explained Step-by-Step
If you’ve ever sat with a Data Structures & Algorithms (DSA) – dynamic programming (DP) problem for hours, scratching your head, you’re not alone. Many students (including me, once upon a time) hear the word “DP” and think it’s some mystical topic that only experts can handle. But here’s the good news: DP isn’t magic. It’s just problem-solving with a little extra memory.
Let’s walk through it slowly, step by step, without throwing in heavy jargon.
What is Dynamic Programming, Really?
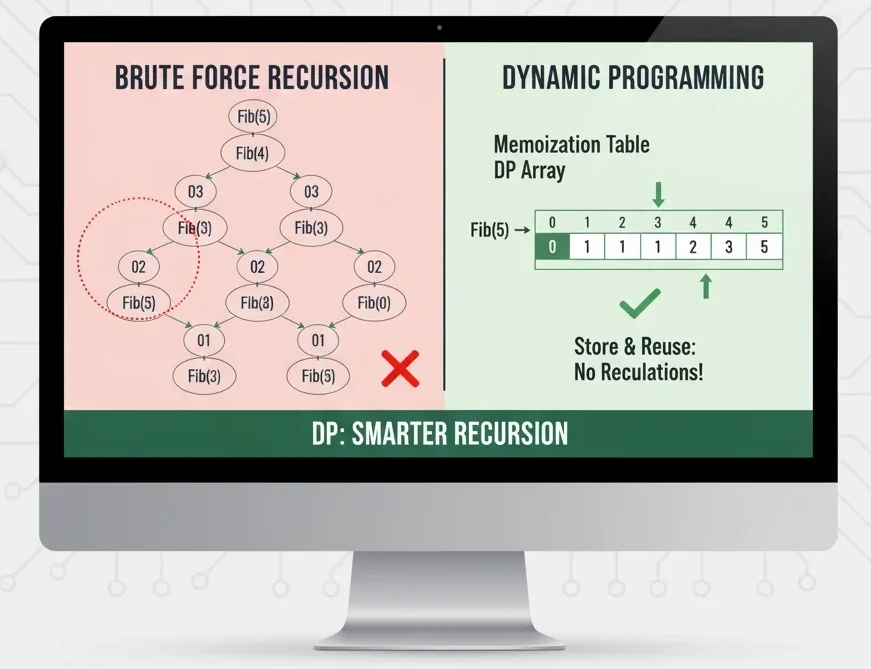
Dynamic Programming is nothing but a smarter way to solve problems where the same sub-problems keep repeating. Instead of solving them again and again, you store the answers and reuse them.
Think of it like this: imagine you’re preparing for an exam and you’ve already solved a tricky math problem once. If the same question comes again, will you redo the whole calculation? Of course not. You’ll check your notebook where you wrote the solution. That’s DP in a nutshell.
Step 1: Identify Overlapping Subproblems in Data Structures & Algorithms (DSA) – dynamic programming (DP)
The first step is spotting whether DP is even needed. Many problems don’t need it.
Take the Fibonacci series:
F(n) = F(n-1) + F(n-2)
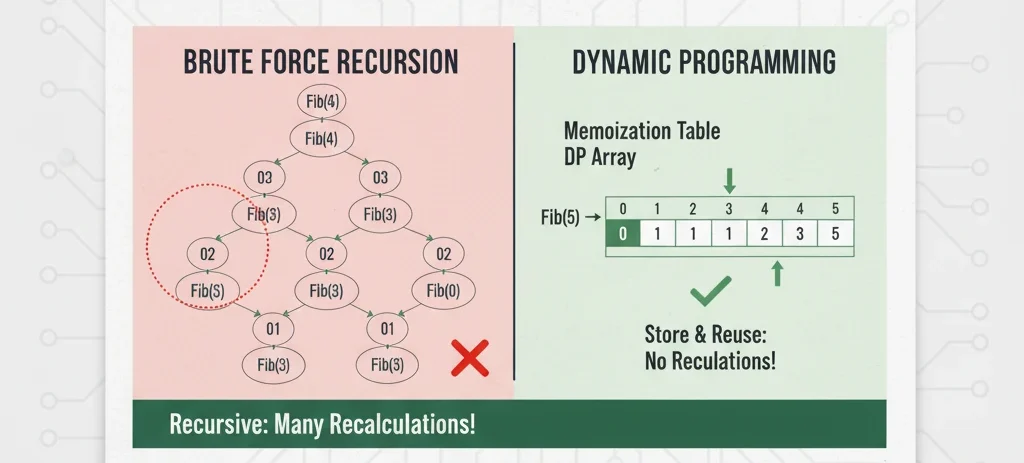
If you write a plain recursive function, it will calculate the same Fibonacci numbers again and again. For example, while calculating F(5), it will separately compute F(3) multiple times. Waste of time, right?
That’s where DP saves the day. Store the results, and next time you need them, just look them up.
Step 2: Two Main Approaches in dynamic programming (DP)
There are two common DP styles:
- Top-Down (Memoization) – You write the recursive solution as usual but keep a dictionary/array to store results of solved sub-problems. Next time the function is called with the same input, it directly returns the stored value.
- Bottom-Up (Tabulation) – Instead of recursion, you start solving from the smallest sub-problems and build your way up. Usually done with loops and arrays.
For beginners, memoization feels easier because it looks similar to normal recursion. But as you practice, bottom-up often becomes faster and cleaner.
Step 3: Break Down with Examples in dynamic programming (DP)
Example 1: Fibonacci Numbers
- Naive recursion: exponential time.
- With DP (memoization): O(n).
Python Fibonacci Code
def fib(n, dp):
if n <= 1:
return n
if dp[n] != -1:
return dp[n]
dp[n] = fib(n-1, dp) + fib(n-2, dp)
return dp[n]
n = 10
dp = [-1] * (n+1)
print("fib(", n, ") =", fib(n, dp))
Run on Programiz
Example 2: The Classic “Knapsack Problem” in dynamic programming (DP)
You have a bag with limited weight capacity and items with given weights and values. The question: how do you maximize the value without exceeding capacity?
Here’s how DP helps:
- At every step, you decide: take the item or leave it.
- If you take it, reduce capacity and add its value.
- If you skip it, move on to the next item.
Without DP, this explodes into many repeated choices. With DP, you store results of (current_index, remaining_capacity) so you don’t redo them.
This example is why DP is loved in competitive programming and interviews.
Step 4: Recognize Common Patterns in dynamic programming (DP)
Most DP problems fall into certain patterns. Spotting them saves a lot of time. Some popular ones:
- Fibonacci-like problems – climbing stairs, tiling, etc.
- Knapsack-type – subset sums, partition problems.
- Grid-based DP – unique paths, minimum path sum.
- String DP – longest common subsequence, edit distance.
The trick is not to memorize solutions but to recognize which category a new problem belongs to.
Step 5: Practice Gradually in dynamic programming (DP)
Don’t jump directly into tough problems. Start small. A good roadmap:
- Fibonacci, climbing stairs, simple grid problems.
- Knapsack, coin change, partition problems.
- Longest common subsequence, edit distance.
- More advanced DP like matrix chain multiplication or DP on trees.
Every solved problem adds to your “pattern library.
Why Students Struggle with DP
- Overthinking: Many treat DP as a brand-new subject, instead of just an extension of recursion.
- Memorizing code: Doesn’t work. You need to understand why the states are stored.
- Fear of complexity: Yes, some DP problems look scary. But the easiest way to get better is to keep solving.
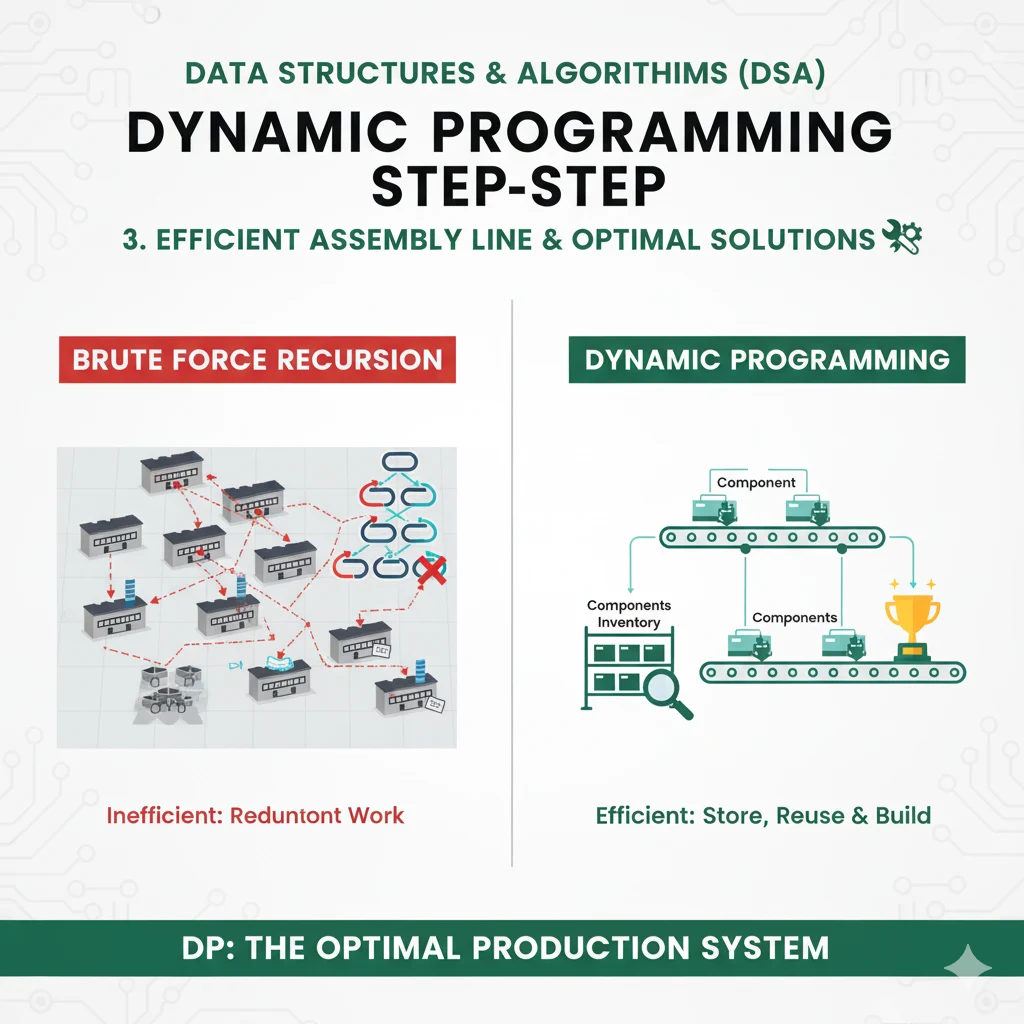
Final Thoughts
Dynamic Programming isn’t about learning fancy formulas. It’s about avoiding repeated work. That’s it.
Next time you see a problem, ask:
- Does it break into smaller subproblems?
- Do those subproblems repeat?
- Can I store and reuse results?
If yes, you’ve got yourself a DP problem. Start small, write code, make mistakes, debug, and improve. Over time, the patterns will click, and you’ll realize DP is not a monster but a powerful friend in problem-solving.
To strengthen your basics, don’t miss our complete guide on Analysis of Algorithm in Data Structure

3 thoughts on “Data Structures & Algorithms (DSA) – Dynamic Programming Explained Step-by-Step”